Granular Gas Research in the Sibley School
Grains interacting through binary collisions behave as a
"granular gas," see for example this movie of shaken steel spheres
(ball bearings)
held in a small transparent
box free-floating that we recorded in the reduced gravity
environment of NASA's KC-135
microgravity aircraft. In a granular gas, grains interact through "binary" collisions involving two
grains only.
A crucial concept in granular gases is the "granular temperature," resembling the "kinetic energy" k in turbulence, and measuring the fluctuation energy of agitated grains. The granular temperature concept was borrowed from the Maxwell-Boltzmann kinetic theory of gases by Japanese scientists like Ogawa, Kanatani and Oshima in the 1970's, see Campbell and Brennen (1983), and exploited in formal theories of dissipative granular gases by scientists like Savage, Lun, Jenkins, Ackermann, Haff, Shen, Jackson, and others in the 1980's, and more recently by Dufty, Goldhirsch, Hayakawa, Kumaran, Garzo, Hrenya, Behringer, Kondic, and others.
A challenge to theory is the formation of particle clusters. The following article points to recent progress by Mitrano et al (2014) on the subject of clusters: M.Y. Louge: "The surprising relevance of a continuum description to granular clusters," J. Fluid Mech. 742, 1-4 (2014), doi:10.1017/jfm.2013.650.
Valance, A. and M. Louge (2015) Granular physics (Physique des milieux granulaires), Comptes Rendus Physique, doi:10.1016/j.crhy.2014.11.007, in press.
This article prefaces a special issue on granular physics guest-edited by Alexandre Valance and Michel Louge for Comptes-Rendus Physique, the journal of the French Academy of Sciences.
General Results
Our contributions to this subject include numerical simulations,
theoretical calculations and microgravity experiments. They are
reported in the following publications:
Louge M., Jenkins J.T. and Hopkins M.: “Computer Simulations of Rapid Granular Shear Flows between Parallel Bumpy Boundaries,” Phys. Fluids A 2 (6), 1042-44 (1990).
These numerical simulations of disks between two bumpy walls tested
the theory of Hanes, et al (1988). They confirmed the existence of two
regimes depending whether the boundary is a sink or a source of
fluctuation energy for the flow.
An excerpt of Louge, Jenkins and Hopkins (1990)
is available here.
 Simple shear flows of nearly
elastic disks.
Simple shear flows of nearly
elastic disks.  The
same shear flow, but for inelastic disks.
The
same shear flow, but for inelastic disks. Hopkins, M.A. and Louge M.: “Inelastic Microstructure in Rapid Granular Flows of Smooth Disks,” Phys. Fluids A 3(1), 47-57 (1991).
These numerical simulations of disks in a "Lees-Edwards" periodic
domain were the first to reveal the formation of clusters of particles
in a simple shear flow, see above figure.
An excerpt of Hopkins and Louge (1991)
is available here.
Hopkins M., Jenkins J. and Louge M.: “On the structure of 3D shear flows,” Mechanics of Materials 16, 179-187 (1993).
This paper generalizes the cluster formation observed by Hopkins and Louge to 3D.
M. Louge, J. Jenkins and M.A. Hopkins: “The relaxation of the second moments in rapid shear flows of smooth disks,” Mechanics of Materials, 16, 199-203 (1993).
In this paper, we report numerical simulations of the transient behavior of disks colliding in simple shear flows. The simulations change the shear rate suddenly, and reveal the resulting relaxation of the anisotropic stresses. The simulations test predictions of Jenkins and Richman (1988).
Louge, M.Y.: “Computer simulations of rapid granular flows of Spheres interacting with a flat, frictional boundary”, Phys. Fluids 6, 2253-2269 (1994).
In this paper, we use numerical simulations to test the theory of Jenkins (1992) for the interaction between a rapid granular flow of spheres and a flat, frictional wall. We examine the boundary conditions that relate the shear stress and energy flux at the wall to the normal stress, slip velocity, and fluctuation energy, and to the parameters that characterize a collision. We find that, while Jenkins' theory captures the trends of the boundary conditions at low friction, it does not do well at large friction. A critical evaluation of Jenkins’ assumptions suggests where his theory may be improved. The paper also reports information on velocity distributions, behavior at large wall friction, spin and its fluctuations, spatial distribution near the wall, comparisons with the Henderson, Abraham and Barker (1976) theory, phase transition, and energy dissipation. Zipped source codes for flat, frictional simulations, including the thermostated wall, are available here.
 Sketch of the simulation strategy. Note the
"thermostat" at the upper driving wall.
Sketch of the simulation strategy. Note the
"thermostat" at the upper driving wall. 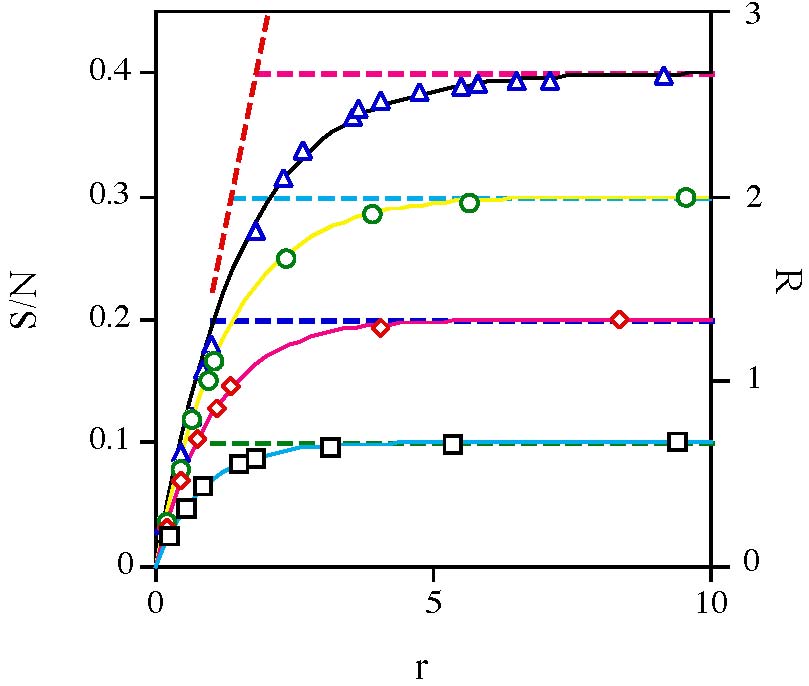 Ratio of shear and normal stress at the flat,
frictional wall versus dimensionless velocity of the contact point.
Ratio of shear and normal stress at the flat,
frictional wall versus dimensionless velocity of the contact point. 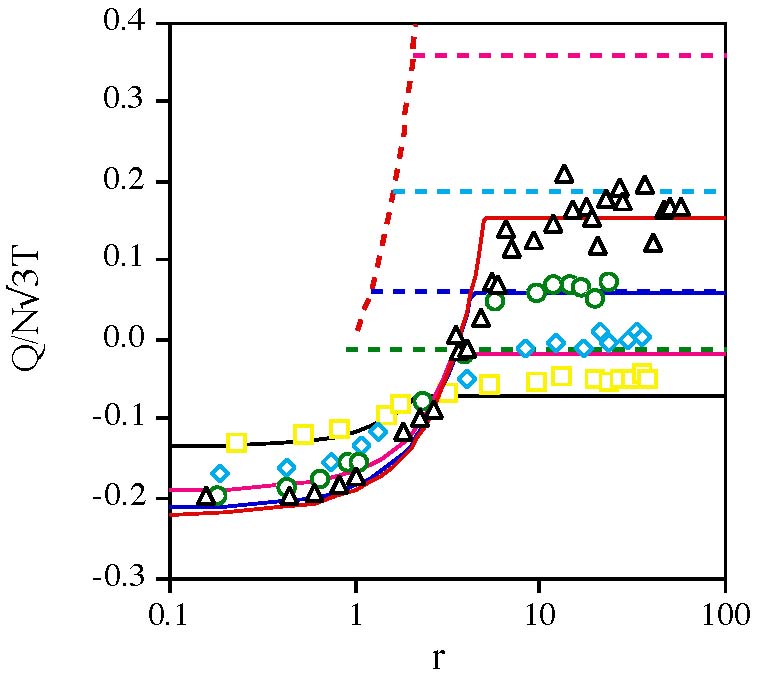 Flux
of fluctuation energy through the wall versus dimensionless velocity of
the contact point.
Flux
of fluctuation energy through the wall versus dimensionless velocity of
the contact point.
A short excerpt of Louge (1994) is available here.
J. T. Jenkins and M. Louge: “On the flux of fluctuation energy in a collisional grain flow at a flat, frictional wall,” Phys. Fluids 9, 2835-2840 (1997).
In this paper, we repair the theory of Jenkins (1992)
to provide more definitive boundary conditions for the flux of
fluctuation energy through a flat, frictional wall holding a granular
gas. We provide closed-form expressions in terms of impact parameters
that can be evaluated independently. Overall, the boundary conditions
for the effective friction and flux of fluctuation energy reported in Eqs. (25), (28) and
(29) of Louge (1994)
are a reliable set for granular gases interacting with the flat,
frictional wall. Because they are expressed in terms of measurable
impact parameters, they should be used instead of heuristic expressions
such as that of Johnson
and Jackson (1987), which involve an adjustable "specularity"
parameter that is not accessible to independent measurements.
A short excerpt of Jenkins and Louge (1997) is
available here.
Microgravity experiments
Because gravitational accelerations tend to "condense" a granular
gas, it is necessary to operate in microgravity to avoid contacts
involving many grains at once. To carry out such experiments, NASA gave
us access to its KC-135 microgravity aircraft from 1998 to 2002.This microgravity project had two principal sub-projects. The first, which focused on gas-solid interactions and is called SiGMA, is described in a separate page. The second, discussed here and called mugSEG (Microgravity Segregation of Energetic Spheres), investigated the segregation of grains by size or mass without signicant influence from the surrounding gas.
In the absence of gravity, the separation of grains by properties - size, for example - is driven by spatial gradients in granular temperature. This is the macroscopic equivalent of the Soret effect, also known as "thermal diffusion" by physical chemists. The segregation of grains by size is commonly observed in geophysical flows and industrial processes. Many mechanisms may be responsible for segregation. Although most of these are strongly influenced by gravity, work on granular segregation in rotating drums, for example, have suggested that segregation in directions transverse to gravity can be captured by kinetic theories designed for gravity-free environments.
We carried out microgravity experiments in a race-track shear cell and an axisymmetric shear cell. Movies of the two systems are shown below.
Our principal results from microgravity experiments are reported in the following papers:
H. Xu, M. Louge and A. Reeves: “Solutions of the Kinetic Theory for Bounded Collisional Granular Flows,” Continuum Mechanics and Thermodynamics 15: 321–349 (2003).
This relatively long paper summarizes our microgravity experiments, theory and numerical simulations on granular gases. It contains the first (and so far only) side-by-side comparison of results from these three activities on a well-defined three-dimensional granular system, in which all granular properties are measured independently.
The paper provides practical information on the form of the non-linear governing equations, the numerical method of their resolution, new boundary conditions for bumpy, frictional walls, the description of an integral method to analyze narrow channels, a discussion of the effects of centripetal accelerations, a description of the computer vision tracking algorithm used in the microgravity experiments, an application to temperature-gradient-driven granular segregation, a description of a simplified theory to make the segregtion problem more tractable, and, finally, the direct comparison of microgravity segregation experiments, numerical simulations and theory.
Additional information on interactions
of agitated grains with a gas can be found in Xu,
Verberg, Koch and Louge (2009), and in Haitao Xu's
thesis. MATLAB programs solving the equations of the kinetic theory can be downloaded here.
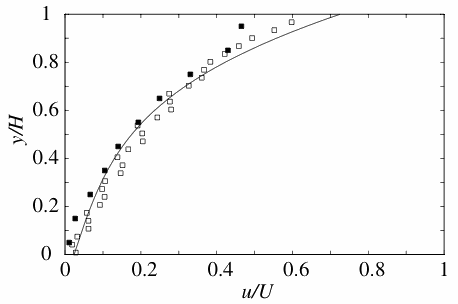 Profiles
of velocity across the microgravity shear cell; closed symbols are
data, open symbols are simulations and line is theory.
Profiles
of velocity across the microgravity shear cell; closed symbols are
data, open symbols are simulations and line is theory. 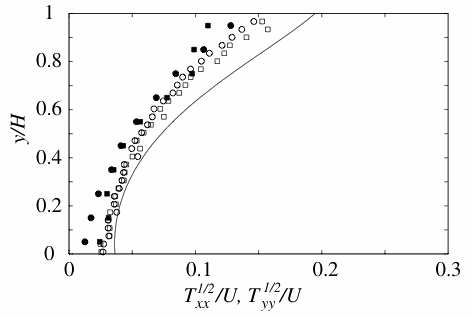 Profiles of granular temperature in the
microgravity shear cell; lines and symbols, see left figure.
Profiles of granular temperature in the
microgravity shear cell; lines and symbols, see left figure.
H. Xu, A. P. Reeves and M. Y. Louge, “Measurement Errors in the Mean and Fluctuation Velocities of Spherical Grains from a Computer Analysis of Digital Images,” Rev. Sci. Instrum. 75, 811-819 (2004).
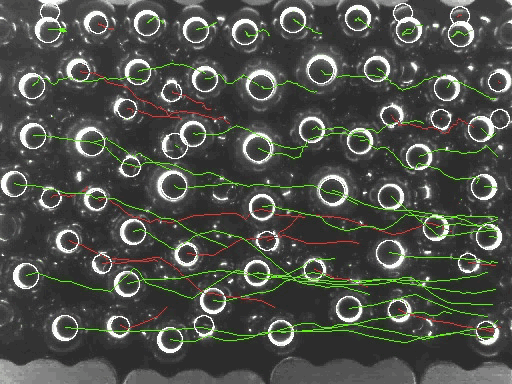
In this paper, we describe a computer vision algorithm to track spheres colliding in microgravity from a sequence of digital images, and to extract their mean and fluctuation velocities.
Crucially, we predict the resulting magniture of errors in evaluating the granular temperature. In many instances found in the literature, such errors are ignored, possibly leading to unrealiable results, particularly when the granular system is dense.
We analyze four kinds of intrinsic errors. The first two artificially reduce the apparent granular temperature. They derive from the inability of the algorithm to track indistinguishable spheres moving with excessive speed, and from invisible collisions occurring between consecutive frames. The third is due to the finite pixel size. The resulting uncertainty in the position of the spheres increases the measured granular temperature. The last arises from the partitioning of the flow domain in strips to calculate velocity profiles. While this last kind of error can always be reduced by increasing the number of images acquired, the first three cannot be made arbitrarily small without improving pixel resolution. Using microgravity experiments and numerical simulations of a shear flow, we illustrate insidious distortions of the mean and fluctuation velocity profiles that originate with the unavoidable errors that we have discussed.
![]()
Click on the image to animate the tracking of ceramic (white) and
acrylic (dark) spheres.
of grains in the race track shear cell (movie: Chris Pelkie). Simulations were created with the source code that may be downloaded here. A movie of the experiment is shown here. It was recorded during
a KC-135 parabola like this one.
 Left to right: Peter Weisz, Enrique Ramé
and Michel Louge on the KC-135.
Left to right: Peter Weisz, Enrique Ramé
and Michel Louge on the KC-135. NASA's
KC-135 on a snow-
NASA's
KC-135 on a snow-covered taxiway at the Glenn Research Center
Conference papers
M. Louge and H. Xu: “Collisional Granular Flows with and without Gas Interactions in Microgravity,” in Mechanics of the 21st Century, W. Gutkowski and T.A. Kowalewski, eds., Springer, Dortrecht, The Netherlands (2005), pp. 229-240.
This paper provides additional information on granular and granular-fluid microgravity experiments and theories at Cornell.
H. Xu, M. Louge and J. T. Jenkins, “Flow development of a sheared collisional granular flow,” in Powders and Grains 2001, Y. Kishino, ed., Swets & Zeitlinger, Lisse, pp. 359-362 (2001).
H. Xu, M. Louge and J. Jenkins: “Flow development of a gas-solid suspension in a microgravity Couette apparatus,” AIAA paper 2001-4992, session FP-3, KSC Conference on International Space Station Utilization, October 15-18, 2001.
The two preceding papers analyze flow development in a narrow channel using an integral method.
M. Louge, J. Jenkins, H. Xu and B. Arnarson, “Granular segregation in collisional shearing flows,” in: Mechanics for a New Millennium, A. Aref and J.W. Phillips, eds., Kluver Academic Publishers (2001), pp. 239-252.
This paper outlines theory, simulations and experiments with binary granular mixtures in microgravity. It reports results obtained on NASA's KC-135 microgravity aircraft.
M.Y. Louge, J.T. Jenkins, A. Reeves and S. Keast: “Microgravity segregation in collisional granular shearing flows,” Proceedings of the IUTAM Symposium on Segregation in Granular Materials, A.D. Rosato and D.L. Blackmore, eds., Kluver Academic Publishers, Boston (2000), pp. 103-112.
This paper reports results obtained on NASA's KC-135 microgravity aircraft.
R.A. Wilkinson, R.P. Behringer, J.T. Jenkins and M.Y. Louge, "Granular materials and the risks they pose for success on the Moon and Mars," Space Technology and Applications International Forum 2005, American Institute of Physics (2005).
This paper warns of the risks in sending long-term missions to the Moon and Mars without basic understanding of granular mechanics.
M. Louge, H. Xu and J. T. Jenkins, “Studies of Gas-particle Interactions in a Microgravity Flow Cell,” in Powders and Grains 2001, Y. Kishino, ed., Swets & Zeitlinger, Lisse, pp. 557-560 (2001).
H. Xu, M. Louge and J. Jenkins: “Flow development of a gas-solid suspension in a microgravity Couette apparatus,” AIAA paper 2001-4992, session FP-3, KSC Conference on International Space Station Utilization, October 15-18, 2001.
The two preceding papers summarize our strategy for studying gas-particle interactions in microgravity.
Miscellaneous information
Download here a manuscript explaining how to infer solid volume fraction
of a suspension of spheres from observations through flat optical
windows, such as those used in our mugSEG or SiGMA experiments. The
calculation exploits the Henderson-Abraham-Barker (1976) for the
spatial distribution of spheres close to a flat wall.